Let's solve an option pricing puzzle
Alpaca Markets provides a platform for algorithmic trading with dedicated APIs. Historically, they only supported cash Equity and Crypto assets on their platform. They are looking to expand the list of assets they support, and you can imagine how excited I was when I saw they launched a waitlist for getting early access to their options trading API. Anyone can sign up for the preview, but Alpaca will give priority access and $99 credit for a premium account subscription to highly motivated users who can solve a special puzzle. Puzzles involving options make me feel giddy - let's solve it!
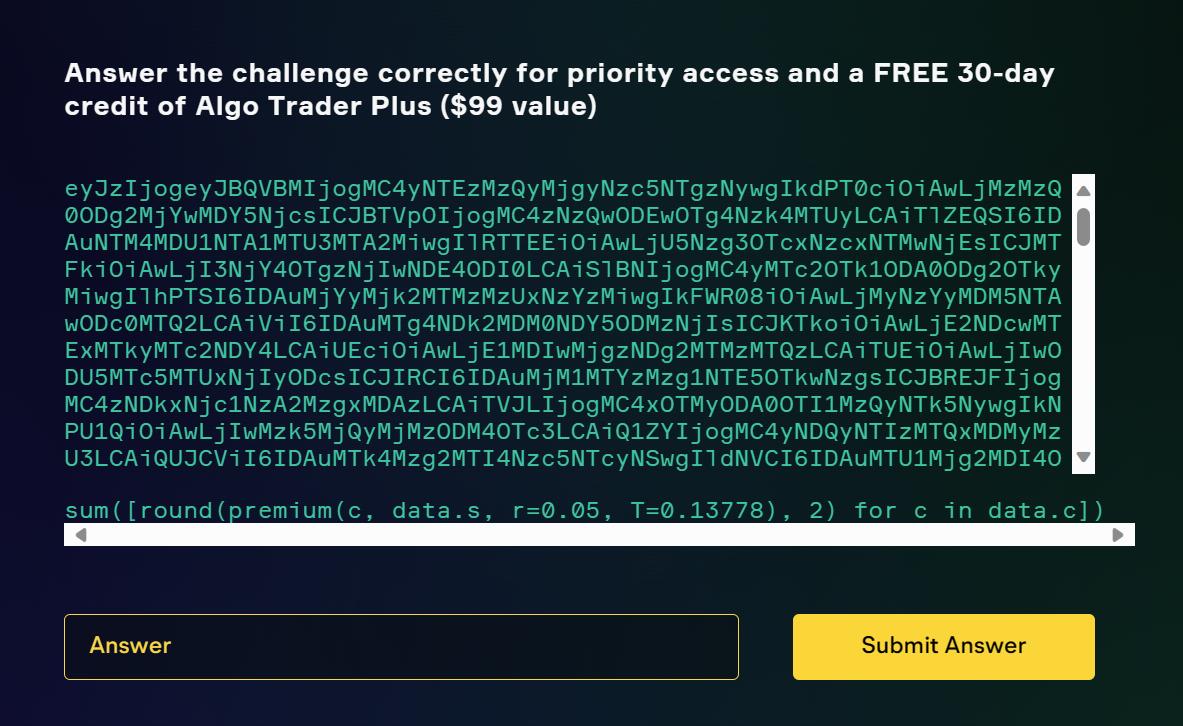
The puzzle
eyJzIjogeyJBQVBMIjogMC4yNTEzMzQyMjgyNzc5NTgzNywgIkdPT0ciOiAwLjMzMzQ0ODg2MjYwMDY5NjcsICJBTVpOIjogMC4zNzQwODEwOTg4Nzk4MTUyLCAiTlZEQSI6IDAuNTM4MDU1NTA1MTU3MTA2MiwgIlRTTEEiOiAwLjU5Nzg3OTcxNzcxNTMwNjEsICJMTFkiOiAwLjI3NjY4OTgzNjIwNDE4ODI0LCAiSlBNIjogMC4yMTc2OTk1ODA0ODg2OTkyMiwgIlhPTSI6IDAuMjYyMjk2MTMzMzUxNzYzMiwgIkFWR08iOiAwLjMyNzYyMDM5NTAwODc0MTQ2LCAiViI6IDAuMTg4NDk2MDM0NDY5ODMzNjIsICJKTkoiOiAwLjE2NDcwMTExMTkyMTc2NDY4LCAiUEciOiAwLjE1MDIwMjgzNDg2MTMzMTQzLCAiTUEiOiAwLjIwODU5MTc5MTUxNjIyODcsICJIRCI6IDAuMjM1MTYzMzg1NTE5OTkwNzgsICJBREJFIjogMC4zNDkxNjc1NzA2MzgxMDAzLCAiTVJLIjogMC4xOTMyODA0OTI1MzQyNTk5NywgIkNPU1QiOiAwLjIwMzk5MjQyMjMzODM4OTc3LCAiQ1ZYIjogMC4yNDQyNTIzMTQxMDMyMzU3LCAiQUJCViI6IDAuMTk4Mzg2MTI4Nzc5NTcyNSwgIldNVCI6IDAuMTU1Mjg2MDI4ODQ2OTMxNzcsICJQRVAiOiAwLjE1MTE0NzI4MzUxMDg2NjQsICJLTyI6IDAuMTQxOTI1MjE3OTc0MDMzMTgsICJDU0NPIjogMC4xOTc5ODI0NDkzNTI1NTk0MywgIkNSTSI6IDAuMzQzNjEzNzk5MTgwNzUyOTcsICJBQ04iOiAwLjI2MzIyOTE3NzcxMzgxMzE2LCAiTkZMWCI6IDAuNDIyNTg1NDIwODM0MzQxMzYsICJNQ0QiOiAwLjEzOTczNTQwNzAwNTU0NTcsICJMSU4iOiAwLjIwMjgzMzk4NDQxMTQxMjU3LCAiQU1EIjogMC40OTM5NTA1MDA2NzUxNjQ2LCAiQkFDIjogMC4yNjIzODI1OTU5Mzc4NjMwNiwgIk9SQ0wiOiAwLjI3NzIwNTIwODc1MDU1NDY1LCAiQ01DU0EiOiAwLjI1Mjc4NTQ4MjI2MDkyNTg0LCAiUEZFIjogMC4yMTc2ODkwODU4ODU3MjUzMywgIkFCVCI6IDAuMjExOTMyMzI3MDAzNzgxNTYsICJJTlRDIjogMC4zODg4MDQzMDQyOTQwOTQ0NiwgIkRJUyI6IDAuMzE3MjM5OTEwMDg4NzYxNCwgIlZaIjogMC4yNDE0MTAwMDc1NjYwMjIwMiwgIldGQyI6IDAuMjc4NzY0NjE0MjI2NDY3ODcsICJJTlRVIjogMC4zNDQ3NzIxMzkyNTk5OTcyLCAiQU1HTiI6IDAuMjExMTM1OTk4NjY1MzI5NDIsICJQTSI6IDAuMTc2NTEzMzAwNTU1MDk4NDIsICJRQ09NIjogMC4zNTk3ODQ3OTE0MTc0MTcxNSwgIkNPUCI6IDAuMzE0OTU4MTAyNjg5MDI4NCwgIklCTSI6IDAuMTc2OTc4Nzg1MTM2NTc4MDUsICJTUFkiOiAwLjE1NzAwNjg0MTM3NTMzMzIyLCAiUVFRIjogMC4yMTMxMzgxNTM1OTM0NzY3NH0sICJjIjogeyJBQVBMMjMxMjI5QzAwMTg1MDAwIjogeyJTIjogMTg4LjAxLCAiSyI6IDE4NS4wfSwgIkdPT0cyMzEyMjlDMDAxMzYwMDAiOiB7IlMiOiAxMzYuMzgsICJLIjogMTM2LjB9LCAiQU1aTjIzMTIyOUMwMDE0MzAwMCI6IHsiUyI6IDE0My4yLCAiSyI6IDE0My4wfSwgIk5WREEyMzEyMjlDMDA0ODUwMDAiOiB7IlMiOiA0ODguODgsICJLIjogNDg1LjB9LCAiVFNMQTIzMTIyOUMwMDI0MDAwMCI6IHsiUyI6IDI0Mi44NCwgIksiOiAyNDAuMH0sICJMTFkyMzEyMjlDMDA1ODUwMDAiOiB7IlMiOiA1ODguNTQsICJLIjogNTg1LjB9LCAiSlBNMjMxMjI5QzAwMTQ5MDAwIjogeyJTIjogMTQ5Ljc0LCAiSyI6IDE0OS4wfSwgIlhPTTIzMTIyOVAwMDEwNDAwMCI6IHsiUyI6IDEwMy42NiwgIksiOiAxMDQuMH0sICJBVkdPMjMxMjI5QzAwOTc1MDAwIjogeyJTIjogOTc1LjQsICJLIjogOTc1LjB9LCAiVjIzMTIyOUMwMDI0NTAwMCI6IHsiUyI6IDI0OC4xMSwgIksiOiAyNDUuMH0sICJKTkoyMzEyMjlDMDAxNDUwMDAiOiB7IlMiOiAxNDguOCwgIksiOiAxNDUuMH0sICJQRzIzMTIyOVAwMDE0NTAwMCI6IHsiUyI6IDE1MS40MiwgIksiOiAxNDUuMH0sICJNQTIzMTIyOVAwMDM5NTAwMCI6IHsiUyI6IDM5Ni44MywgIksiOiAzOTUuMH0sICJIRDIzMTIyOUMwMDMwNTAwMCI6IHsiUyI6IDMwOC4xOSwgIksiOiAzMDUuMH0sICJBREJFMjMxMjI5UDAwNTkwMDAwIjogeyJTIjogNTk1LjMxLCAiSyI6IDU5MC4wfSwgIk1SSzIzMTIyOVAwMDEwMjAwMCI6IHsiUyI6IDEwMS4zNSwgIksiOiAxMDIuMH0sICJDT1NUMjMxMjI5QzAwNTk1MDAwIjogeyJTIjogNTk2Ljc4LCAiSyI6IDU5NS4wfSwgIkNWWDIzMTIyOUMwMDE0NTAwMCI6IHsiUyI6IDE0NS41NiwgIksiOiAxNDUuMH0sICJBQkJWMjMxMjI5UDAwMTM4MDAwIjogeyJTIjogMTM3LjYsICJLIjogMTM4LjB9LCAiV01UMjMxMjI5QzAwMTY1MDAwIjogeyJTIjogMTY5Ljc4LCAiSyI6IDE2NS4wfSwgIlBFUDIzMTIyOUMwMDE2NTAwMCI6IHsiUyI6IDE2Ny4yNSwgIksiOiAxNjUuMH0sICJLTzIzMTIyOUMwMDA1NzAwMCI6IHsiUyI6IDU3LjIxLCAiSyI6IDU3LjB9LCAiQ1NDTzIzMTIyOUMwMDA1MzAwMCI6IHsiUyI6IDUzLjI4LCAiSyI6IDUzLjB9LCAiQ1JNMjMxMjI5UDAwMjIwMDAwIjogeyJTIjogMjE5LjQyLCAiSyI6IDIyMC4wfSwgIkFDTjIzMTIyOUMwMDMzNTAwMCI6IHsiUyI6IDMyNS41LCAiSyI6IDMzNS4wfSwgIk5GTFgyMzEyMjlDMDA0NjAwMDAiOiB7IlMiOiA0NjEuOTQsICJLIjogNDYwLjB9LCAiTUNEMjMxMjI5UDAwMjY1MDAwIjogeyJTIjogMjcwLjM5LCAiSyI6IDI2NS4wfSwgIkFNRDIzMTIyOVAwMDExOTAwMCI6IHsiUyI6IDExOC4wLCAiSyI6IDExOS4wfSwgIkJBQzIzMTIyOUMwMDAzMDAwMCI6IHsiUyI6IDI5LjYyLCAiSyI6IDMwLjB9LCAiT1JDTDIzMTIyOVAwMDExMTAwMCI6IHsiUyI6IDExNC4wNiwgIksiOiAxMTEuMH0sICJDTUNTQTIzMTIyOUMwMDA0MjAwMCI6IHsiUyI6IDQyLjUzLCAiSyI6IDQyLjB9LCAiUEZFMjMxMjI5QzAwMDMwMDAwIjogeyJTIjogMzAuMTksICJLIjogMzAuMH0sICJBQlQyMzEyMjlDMDAwOTgwMDAiOiB7IlMiOiA5OC4wLCAiSyI6IDk4LjB9LCAiSU5UQzIzMTIyOUMwMDA0MDAwMCI6IHsiUyI6IDQwLjYxLCAiSyI6IDQwLjB9LCAiRElTMjMxMjI5QzAwMDkzMDAwIjogeyJTIjogOTMuOTMsICJLIjogOTMuMH0sICJWWjIzMTIyOUMwMDAzNTAwMCI6IHsiUyI6IDM2LjAsICJLIjogMzUuMH0sICJXRkMyMzEyMjlDMDAwNDIwMDAiOiB7IlMiOiA0Mi44NCwgIksiOiA0Mi4wfSwgIkFNR04yMzEyMjlDMDAyNzAwMDAiOiB7IlMiOiAyNzMuMDMsICJLIjogMjcwLjB9LCAiUUNPTTIzMTIyOUMwMDEyODAwMCI6IHsiUyI6IDEyOC45MiwgIksiOiAxMjguMH0sICJDT1AyMzEyMjlQMDAxMTYwMDAiOiB7IlMiOiAxMTUuMDMsICJLIjogMTE2LjB9LCAiSUJNMjMxMjI5QzAwMTUyNTAwIjogeyJTIjogMTUyLjU4LCAiSyI6IDE1Mi41fSwgIlNQWTIzMTIyOUMwMDQ0OTAwMCI6IHsiUyI6IDQ0OS42OCwgIksiOiA0NDkuMH0sICJRUVEyMzEyMjlDMDAzNDkwMDAiOiB7IlMiOiAzODUuNjIsICJLIjogMzQ5LjB9fX0=
sum([round(premium(c, data.s, r=0.05, T=0.13778), 2) for c in data.c])
The expected answer appears to be a single number, which is derived by taking the sum of a the rounded output (to two decimals) of a function called premium, applied on a collection of records stored in an object named data.c. It's probably safe to assume at this point that the data object is likely stored in the encrypted string above. There is quite a lot of information we can infer just by looking at the choice of variable naming:
- In the field of quantitative finance, the price of an option is often referred to as "premium".
- The
premiumfunction described above takes four parameters, but two of them are explicitly named: $r$ and $T$ - One of the most commonly known and used formulas to price options which takes, amogst others, parameters named $r$ and $T$ is the famous Black-Scholes formula.
- Knowing we are dealing with Black-Scholes allows us to better define the variables in the
premiumfunction. $r$ is the "risk free" rate, which is used to discount asset prices or cash flows present value. $T$ is the time to expiry, expressed in years (technically, in the Black-Scholes formula, the time to expiry component is calculated as $(T-t)$, but I assume that they simply refer to it as $T$ here). We will look at Black-Scholes in more detail in the next section. canddata.slikely contain the other variables needed by Black-Scholes to produce an option price (or premium).
I've been doing software engineering for a while, so my eyes are kind of trained to spot various types of common encoding techniques. I suspected the string at the top was encoded with Base64 - which turned out to be true. Although I'm sure ChatGPT could have figured that out, too. Let's look at what the decoded output looks like:
import base64
import json
b64_str = "eyJzIjogeyJBQVBMIjogMC4yNTEzMzQyMjgyNzc5NTgzNywgIkdPT0ciOiAwLjMzMzQ0ODg2MjYwMDY5NjcsICJBTVpOIjogMC4zNzQwODEwOTg4Nzk4MTUyLCAiTlZEQSI6IDAuNTM4MDU1NTA1MTU3MTA2MiwgIlRTTEEiOiAwLjU5Nzg3OTcxNzcxNTMwNjEsICJMTFkiOiAwLjI3NjY4OTgzNjIwNDE4ODI0LCAiSlBNIjogMC4yMTc2OTk1ODA0ODg2OTkyMiwgIlhPTSI6IDAuMjYyMjk2MTMzMzUxNzYzMiwgIkFWR08iOiAwLjMyNzYyMDM5NTAwODc0MTQ2LCAiViI6IDAuMTg4NDk2MDM0NDY5ODMzNjIsICJKTkoiOiAwLjE2NDcwMTExMTkyMTc2NDY4LCAiUEciOiAwLjE1MDIwMjgzNDg2MTMzMTQzLCAiTUEiOiAwLjIwODU5MTc5MTUxNjIyODcsICJIRCI6IDAuMjM1MTYzMzg1NTE5OTkwNzgsICJBREJFIjogMC4zNDkxNjc1NzA2MzgxMDAzLCAiTVJLIjogMC4xOTMyODA0OTI1MzQyNTk5NywgIkNPU1QiOiAwLjIwMzk5MjQyMjMzODM4OTc3LCAiQ1ZYIjogMC4yNDQyNTIzMTQxMDMyMzU3LCAiQUJCViI6IDAuMTk4Mzg2MTI4Nzc5NTcyNSwgIldNVCI6IDAuMTU1Mjg2MDI4ODQ2OTMxNzcsICJQRVAiOiAwLjE1MTE0NzI4MzUxMDg2NjQsICJLTyI6IDAuMTQxOTI1MjE3OTc0MDMzMTgsICJDU0NPIjogMC4xOTc5ODI0NDkzNTI1NTk0MywgIkNSTSI6IDAuMzQzNjEzNzk5MTgwNzUyOTcsICJBQ04iOiAwLjI2MzIyOTE3NzcxMzgxMzE2LCAiTkZMWCI6IDAuNDIyNTg1NDIwODM0MzQxMzYsICJNQ0QiOiAwLjEzOTczNTQwNzAwNTU0NTcsICJMSU4iOiAwLjIwMjgzMzk4NDQxMTQxMjU3LCAiQU1EIjogMC40OTM5NTA1MDA2NzUxNjQ2LCAiQkFDIjogMC4yNjIzODI1OTU5Mzc4NjMwNiwgIk9SQ0wiOiAwLjI3NzIwNTIwODc1MDU1NDY1LCAiQ01DU0EiOiAwLjI1Mjc4NTQ4MjI2MDkyNTg0LCAiUEZFIjogMC4yMTc2ODkwODU4ODU3MjUzMywgIkFCVCI6IDAuMjExOTMyMzI3MDAzNzgxNTYsICJJTlRDIjogMC4zODg4MDQzMDQyOTQwOTQ0NiwgIkRJUyI6IDAuMzE3MjM5OTEwMDg4NzYxNCwgIlZaIjogMC4yNDE0MTAwMDc1NjYwMjIwMiwgIldGQyI6IDAuMjc4NzY0NjE0MjI2NDY3ODcsICJJTlRVIjogMC4zNDQ3NzIxMzkyNTk5OTcyLCAiQU1HTiI6IDAuMjExMTM1OTk4NjY1MzI5NDIsICJQTSI6IDAuMTc2NTEzMzAwNTU1MDk4NDIsICJRQ09NIjogMC4zNTk3ODQ3OTE0MTc0MTcxNSwgIkNPUCI6IDAuMzE0OTU4MTAyNjg5MDI4NCwgIklCTSI6IDAuMTc2OTc4Nzg1MTM2NTc4MDUsICJTUFkiOiAwLjE1NzAwNjg0MTM3NTMzMzIyLCAiUVFRIjogMC4yMTMxMzgxNTM1OTM0NzY3NH0sICJjIjogeyJBQVBMMjMxMjI5QzAwMTg1MDAwIjogeyJTIjogMTg4LjAxLCAiSyI6IDE4NS4wfSwgIkdPT0cyMzEyMjlDMDAxMzYwMDAiOiB7IlMiOiAxMzYuMzgsICJLIjogMTM2LjB9LCAiQU1aTjIzMTIyOUMwMDE0MzAwMCI6IHsiUyI6IDE0My4yLCAiSyI6IDE0My4wfSwgIk5WREEyMzEyMjlDMDA0ODUwMDAiOiB7IlMiOiA0ODguODgsICJLIjogNDg1LjB9LCAiVFNMQTIzMTIyOUMwMDI0MDAwMCI6IHsiUyI6IDI0Mi44NCwgIksiOiAyNDAuMH0sICJMTFkyMzEyMjlDMDA1ODUwMDAiOiB7IlMiOiA1ODguNTQsICJLIjogNTg1LjB9LCAiSlBNMjMxMjI5QzAwMTQ5MDAwIjogeyJTIjogMTQ5Ljc0LCAiSyI6IDE0OS4wfSwgIlhPTTIzMTIyOVAwMDEwNDAwMCI6IHsiUyI6IDEwMy42NiwgIksiOiAxMDQuMH0sICJBVkdPMjMxMjI5QzAwOTc1MDAwIjogeyJTIjogOTc1LjQsICJLIjogOTc1LjB9LCAiVjIzMTIyOUMwMDI0NTAwMCI6IHsiUyI6IDI0OC4xMSwgIksiOiAyNDUuMH0sICJKTkoyMzEyMjlDMDAxNDUwMDAiOiB7IlMiOiAxNDguOCwgIksiOiAxNDUuMH0sICJQRzIzMTIyOVAwMDE0NTAwMCI6IHsiUyI6IDE1MS40MiwgIksiOiAxNDUuMH0sICJNQTIzMTIyOVAwMDM5NTAwMCI6IHsiUyI6IDM5Ni44MywgIksiOiAzOTUuMH0sICJIRDIzMTIyOUMwMDMwNTAwMCI6IHsiUyI6IDMwOC4xOSwgIksiOiAzMDUuMH0sICJBREJFMjMxMjI5UDAwNTkwMDAwIjogeyJTIjogNTk1LjMxLCAiSyI6IDU5MC4wfSwgIk1SSzIzMTIyOVAwMDEwMjAwMCI6IHsiUyI6IDEwMS4zNSwgIksiOiAxMDIuMH0sICJDT1NUMjMxMjI5QzAwNTk1MDAwIjogeyJTIjogNTk2Ljc4LCAiSyI6IDU5NS4wfSwgIkNWWDIzMTIyOUMwMDE0NTAwMCI6IHsiUyI6IDE0NS41NiwgIksiOiAxNDUuMH0sICJBQkJWMjMxMjI5UDAwMTM4MDAwIjogeyJTIjogMTM3LjYsICJLIjogMTM4LjB9LCAiV01UMjMxMjI5QzAwMTY1MDAwIjogeyJTIjogMTY5Ljc4LCAiSyI6IDE2NS4wfSwgIlBFUDIzMTIyOUMwMDE2NTAwMCI6IHsiUyI6IDE2Ny4yNSwgIksiOiAxNjUuMH0sICJLTzIzMTIyOUMwMDA1NzAwMCI6IHsiUyI6IDU3LjIxLCAiSyI6IDU3LjB9LCAiQ1NDTzIzMTIyOUMwMDA1MzAwMCI6IHsiUyI6IDUzLjI4LCAiSyI6IDUzLjB9LCAiQ1JNMjMxMjI5UDAwMjIwMDAwIjogeyJTIjogMjE5LjQyLCAiSyI6IDIyMC4wfSwgIkFDTjIzMTIyOUMwMDMzNTAwMCI6IHsiUyI6IDMyNS41LCAiSyI6IDMzNS4wfSwgIk5GTFgyMzEyMjlDMDA0NjAwMDAiOiB7IlMiOiA0NjEuOTQsICJLIjogNDYwLjB9LCAiTUNEMjMxMjI5UDAwMjY1MDAwIjogeyJTIjogMjcwLjM5LCAiSyI6IDI2NS4wfSwgIkFNRDIzMTIyOVAwMDExOTAwMCI6IHsiUyI6IDExOC4wLCAiSyI6IDExOS4wfSwgIkJBQzIzMTIyOUMwMDAzMDAwMCI6IHsiUyI6IDI5LjYyLCAiSyI6IDMwLjB9LCAiT1JDTDIzMTIyOVAwMDExMTAwMCI6IHsiUyI6IDExNC4wNiwgIksiOiAxMTEuMH0sICJDTUNTQTIzMTIyOUMwMDA0MjAwMCI6IHsiUyI6IDQyLjUzLCAiSyI6IDQyLjB9LCAiUEZFMjMxMjI5QzAwMDMwMDAwIjogeyJTIjogMzAuMTksICJLIjogMzAuMH0sICJBQlQyMzEyMjlDMDAwOTgwMDAiOiB7IlMiOiA5OC4wLCAiSyI6IDk4LjB9LCAiSU5UQzIzMTIyOUMwMDA0MDAwMCI6IHsiUyI6IDQwLjYxLCAiSyI6IDQwLjB9LCAiRElTMjMxMjI5QzAwMDkzMDAwIjogeyJTIjogOTMuOTMsICJLIjogOTMuMH0sICJWWjIzMTIyOUMwMDAzNTAwMCI6IHsiUyI6IDM2LjAsICJLIjogMzUuMH0sICJXRkMyMzEyMjlDMDAwNDIwMDAiOiB7IlMiOiA0Mi44NCwgIksiOiA0Mi4wfSwgIkFNR04yMzEyMjlDMDAyNzAwMDAiOiB7IlMiOiAyNzMuMDMsICJLIjogMjcwLjB9LCAiUUNPTTIzMTIyOUMwMDEyODAwMCI6IHsiUyI6IDEyOC45MiwgIksiOiAxMjguMH0sICJDT1AyMzEyMjlQMDAxMTYwMDAiOiB7IlMiOiAxMTUuMDMsICJLIjogMTE2LjB9LCAiSUJNMjMxMjI5QzAwMTUyNTAwIjogeyJTIjogMTUyLjU4LCAiSyI6IDE1Mi41fSwgIlNQWTIzMTIyOUMwMDQ0OTAwMCI6IHsiUyI6IDQ0OS42OCwgIksiOiA0NDkuMH0sICJRUVEyMzEyMjlDMDAzNDkwMDAiOiB7IlMiOiAzODUuNjIsICJLIjogMzQ5LjB9fX0=
b64_decoded = base64.b64decode(b64_str)
decoded_str = bytes.decode(b64_decoded)
data = json.loads(decoded_str)
print(data)
{'s': {'AAPL': 0.25133422827795837,
'GOOG': 0.3334488626006967,
'AMZN': 0.3740810988798152,
'NVDA': 0.5380555051571062,
'TSLA': 0.5978797177153061,
'LLY': 0.27668983620418824,
'JPM': 0.21769958048869922,
'XOM': 0.2622961333517632,
'AVGO': 0.32762039500874146,
'V': 0.18849603446983362,
'JNJ': 0.16470111192176468,
'PG': 0.15020283486133143,
'MA': 0.2085917915162287,
'HD': 0.23516338551999078,
'ADBE': 0.3491675706381003,
'MRK': 0.19328049253425997,
'COST': 0.20399242233838977,
'CVX': 0.2442523141032357,
'ABBV': 0.1983861287795725,
'WMT': 0.15528602884693177,
'PEP': 0.1511472835108664,
'KO': 0.14192521797403318,
'CSCO': 0.19798244935255943,
'CRM': 0.34361379918075297,
'ACN': 0.26322917771381316,
'NFLX': 0.42258542083434136,
'MCD': 0.1397354070055457,
'LIN': 0.20283398441141257,
'AMD': 0.4939505006751646,
'BAC': 0.26238259593786306,
'ORCL': 0.27720520875055465,
'CMCSA': 0.25278548226092584,
'PFE': 0.21768908588572533,
'ABT': 0.21193232700378156,
'INTC': 0.38880430429409446,
'DIS': 0.3172399100887614,
'VZ': 0.24141000756602202,
'WFC': 0.27876461422646787,
'INTU': 0.3447721392599972,
'AMGN': 0.21113599866532942,
'PM': 0.17651330055509842,
'QCOM': 0.35978479141741715,
'COP': 0.3149581026890284,
'IBM': 0.17697878513657805,
'SPY': 0.15700684137533322,
'QQQ': 0.21313815359347674},
'c': {'AAPL231229C00185000': {'S': 188.01, 'K': 185.0},
'GOOG231229C00136000': {'S': 136.38, 'K': 136.0},
'AMZN231229C00143000': {'S': 143.2, 'K': 143.0},
'NVDA231229C00485000': {'S': 488.88, 'K': 485.0},
'TSLA231229C00240000': {'S': 242.84, 'K': 240.0},
'LLY231229C00585000': {'S': 588.54, 'K': 585.0},
'JPM231229C00149000': {'S': 149.74, 'K': 149.0},
'XOM231229P00104000': {'S': 103.66, 'K': 104.0},
'AVGO231229C00975000': {'S': 975.4, 'K': 975.0},
'V231229C00245000': {'S': 248.11, 'K': 245.0},
'JNJ231229C00145000': {'S': 148.8, 'K': 145.0},
'PG231229P00145000': {'S': 151.42, 'K': 145.0},
'MA231229P00395000': {'S': 396.83, 'K': 395.0},
'HD231229C00305000': {'S': 308.19, 'K': 305.0},
'ADBE231229P00590000': {'S': 595.31, 'K': 590.0},
'MRK231229P00102000': {'S': 101.35, 'K': 102.0},
'COST231229C00595000': {'S': 596.78, 'K': 595.0},
'CVX231229C00145000': {'S': 145.56, 'K': 145.0},
'ABBV231229P00138000': {'S': 137.6, 'K': 138.0},
'WMT231229C00165000': {'S': 169.78, 'K': 165.0},
'PEP231229C00165000': {'S': 167.25, 'K': 165.0},
'KO231229C00057000': {'S': 57.21, 'K': 57.0},
'CSCO231229C00053000': {'S': 53.28, 'K': 53.0},
'CRM231229P00220000': {'S': 219.42, 'K': 220.0},
'ACN231229C00335000': {'S': 325.5, 'K': 335.0},
'NFLX231229C00460000': {'S': 461.94, 'K': 460.0},
'MCD231229P00265000': {'S': 270.39, 'K': 265.0},
'AMD231229P00119000': {'S': 118.0, 'K': 119.0},
'BAC231229C00030000': {'S': 29.62, 'K': 30.0},
'ORCL231229P00111000': {'S': 114.06, 'K': 111.0},
'CMCSA231229C00042000': {'S': 42.53, 'K': 42.0},
'PFE231229C00030000': {'S': 30.19, 'K': 30.0},
'ABT231229C00098000': {'S': 98.0, 'K': 98.0},
'INTC231229C00040000': {'S': 40.61, 'K': 40.0},
'DIS231229C00093000': {'S': 93.93, 'K': 93.0},
'VZ231229C00035000': {'S': 36.0, 'K': 35.0},
'WFC231229C00042000': {'S': 42.84, 'K': 42.0},
'AMGN231229C00270000': {'S': 273.03, 'K': 270.0},
'QCOM231229C00128000': {'S': 128.92, 'K': 128.0},
'COP231229P00116000': {'S': 115.03, 'K': 116.0},
'IBM231229C00152500': {'S': 152.58, 'K': 152.5},
'SPY231229C00449000': {'S': 449.68, 'K': 449.0},
'QQQ231229C00349000': {'S': 385.62, 'K': 349.0}}}
This is a simple Python dictionary with a couple of keys: s and c. Before we fully analyze the contents of this dictionary, we would likely benefit from a quick refresher on the Black-Scholes formula, as the data will make a lot more sense once we are equipped with the relevant knowledge.
The Black Scholes Formula
There is a lot of literature on Black-Scholes and what I'm covering in the next couple of paragraphs just scratches the surface. If you find this material interesting, I'd highly recommend you spend more time studying this information from more official resources (ping me if you'd like a list of recommended books/links). And with that said, if you'd like a more elaborate, separate post on Black-Scholes then let me know - I'll gladly write one!
Black-Scholes (technically it's Black-Scholes-Merton, or BSM) is a formula used to price European options. "European" options are options that can only be exercised at expiry. There are other variants such as "American" options, which can be exercised at any point until their expiry, or "Bermudan" options, which can be exercised during pre-defined a window before and up to their expiry.
There are two types of "vanilla" options - put, and call. A call option is the right to buy a particular asset in the future, and at a pre-determined price called the strike. A put option is the right to sell a particular asset in the future, and at a pre-determined price, called - you guessed it - the strike. Both call and put options can be bought or sold. Option contracts have a price, called the "premium". Option buyers pay the premium to the option seller. The Black-Scholes formula allows us to get the price for the option - for both call and put options. See below for the pricing formulas for both:
$$Call(S_{t},t)=\mathcal{N}(d_1) S_{t} - \mathcal{N}(d_2) Ke^{-r(T-t)}$$ $$Put(S_{t},t)=\mathcal{N}(-d_{2})Ke^{-r(T-t)}-\mathcal{N}(-d_{1})S_{t}$$ $$d_{1}=\frac{\ln \frac{S_{t}}{K} + (r + \frac{\sigma^2}{2})(T-t)}{\sigma\sqrt{(T-t)}}$$ $$d_{2}=d_{1}-\sigma\sqrt{(T-t)}$$
The inputs to the Black-Scholes formula are as follows:
- $S_{t}$ - the current spot price of the asset.
- $K$ - the strike price.
- $r$ - the annualized risk free rate.
- $\sigma$ - the implied volatility (expected standard deviation) of the asset throughout the lifetime of the option.
- $\tau = (T-t)$ - the time until the option expiry, measured in years.
Note that the formula above assumes the asset is not paying dividends. If it does, then the annualized dividend yield will also need be an input. One last note here, is that there are a number of variants of the Black-Scholes formula, for different types of assets. The one I present here is for equity assets specifically.
Analyzing the market data and tying it to our pricing function
We mentioned there is a dictionary with two top-level keys: s and c. Let's start with the s key. It holds a nested dictionary with keys that look like company name symbol, and values which look like annualized volatility (implied standard deviation) for some term. The choice for s as the name for this dictionary could be shorthand for "sigma", but I don't really know that for sure. For now, I'll stick to the assumptions that these are annualized volatility numbers.
The c key also holds a nested dictionary as a value. Let's look at the first value of the nested dictionary:
{'AAPL231229C00185000': {'S': 188.01, 'K': 185.0}
The key is AAPL231229C00185000. This looks like an option identifier. The first four characters are AAPL, which stands for the trading symbol of Apple Computers, the company. The next six characters are 231229, which denotes the expiry date of the option: 2023-12-29. The next single character is "C", which stands for "call option" (other entires have "P", which stands for put option), and the last eight characters look like some number. If we quickly analyze the value of the AAPL231229C00185000 key, we see dictionary of {'S': 188.01, 'K': 185.0} which, if you recall from our Black-Scholes section, looks like the spot price of AAPL, denoted by $S$, and the strike of the option, denoted by $K$. We can also see that the value for $K$ - 185.0 - also matches the eight-digit number in the AAPL231229C00185000 key. Going back to the s dictionary, with the example of AAPL, we can see that there is indeed a key for AAPL in the s dictionary. Given the only missing piece of information we need in order to price AAPL231229C00185000 is sigma, I'm now sure that the s dictionary is holding that information, as it has a key for AAPL, with a number of 0.25133422827795837, which is ~25% annuzlied volatility - which seems to be in the right order of magnitude for annualized vol numbers.
In summary, the c dictionary contains option pricing parameters such as the asset name, option type (put or call), option expiry, asset spot price and option strike. Let's see how this ties to the premium function:
sum([round(premium(c, data.s, r=0.05, T=0.13778), 2) for c in data.c])
The premium function takes the following arguments:
c, which we now know contains the spot price $S$, strike $K$, asset name and expirydata.s, which is a dictionary of annualized volatilies for various assets- $r$, the annualized risk-free rate
- $T$, the time to expiry.
A quick thought about the $T$ parameter. Option prices change in value all the time - any change in $S$, $K$, $T$, $r$ and $\sigma$ also affects the option value. This makes answering the puzzle question somewhat tricky because, technically, the correct answer should change every day. Even if we hold all variables other than $T$ constant, $T$ will change with each day that passes. Also, Black-Scholes requires the pricing date, denoted as $t$, as an input, too, as the time to expiry is calculated as $(T-t)$ - option expiry date minus the pricing date - expressed as a floating point number, with 1 being a full calendar year. We don't really seem to have any information about the pricing date, and the expiry information, $T$, provided to us, already seems to be a fraction of a year - so we will go with the assumption that $T$ already factors in the pricing date. It's also common to see Black-Scholes written with the $T$ parameter only, instead of $(T-t)$.
Implementing a solution
import math
import scipy.stats as stats
# Black Scholes option pricing
def bsm(S, K, T, r, sigma, type='C'):
flag = 1 if type == 'C' else -1
# d1 and d2
d1 = (math.log(S / K) + (r + 0.5 * sigma ** 2) * T) / (sigma * math.sqrt(T))
d2 = d1 - sigma * math.sqrt(T)
return flag * (S * stats.norm.cdf(flag * d1, 0.0, 1.0) \
- K * math.exp(-r * T) * stats.norm.cdf(flag * d2, 0.0, 1.0))
This is an implementation of the Black-Scholes formula in a single function call. We added one paramater, called "type", to the function signature. This parameter denotes whether the option we're pricing is a call option or a put option.
Let's go through the first iteration manually: {'AAPL231229C00185000': {'S': 188.01, 'K': 185.0}. We need to parse the ticker into parts. The information we care about is the symbol - AAPL, and the option type - put or call. The expiry date is not needed as we already have a $T$ with the year fraction, which implicitly includes the expiry date. We also don't need the strike value extracted from the ticker, as we have that number given to us in the nested dictionary under the $K$ key. We will still parse all of them, for completeness sake.
If we look at the overall structure of the ticker in data['c'], we can identify as few patterns:
- The expiry date is always 6-characters long, YY-MM-DD
- The strike is always 8-characters long
- The option type is always one character long
- The symbol varies by length (!)
- The order is always symbol-expiry-type-strike
With that information, we can write a parser function:
def parse_ticker(ticker: str):
symbol_end_index = 0
for i in range(len(ticker)):
if ticker[i].isnumeric():
symbol_end_index = i
break
return {"symbol": ticker[:symbol_end_index], "expiry": ticker[symbol_end_index: symbol_end_index + 6], "type": ticker[symbol_end_index + 6], "strike": ticker[symbol_end_index + 6 + 1:]}
Because the symbol length varies, we need to find the index point at which it ends, and the date part begins. This can then be used as an anchor to parse the rest of the values from the ticker, as the rest of the values are fixed in length. This is done in the first for-loop inside the parse_ticker function. Calling the parse_ticker function on AAPL231229C00185000 yields the following:
{'symbol': 'AAPL', 'expiry': '231229', 'type': 'C', 'strike': '00185000'}
We now have all of the information needed to price this option! The volatility number will come from data['s'], which feeds into the premium function. Let's define that function below:
def premium(c, vols, r, T):
ticker, spot_and_strike = c
parsed_data = parse_ticker(ticker)
# Extracting parameters
K = spot_and_strike['K']
S = spot_and_strike['S']
symbol = parsed_data['symbol']
type = parsed_data['type']
sigma = vols[symbol]
# Option premium
premium = bsm(S, K, T, r, sigma, type)
print(f'{symbol}: S={S}, K={K}, r={r}, T={T}, type={type}, sigma={sigma}, premium={premium}')
return premium
Let's talk about the inputs:
cis a tuple of(ticker, {"S"...,"K"...}).volsis simplydata['s'], which contains dictionaries of{symbol:vol}.- $r$ is the annualized risk-free rate.
- $T$ is the time to expiry, expressed as a year fraction.
From these inputs, we are able to get all of the market data needed to pass into the bsm function we created. Recall that both $r$ and $T$ were provided to us as hardcoded numbers in the premium function call described in the puzzle brief. This means that all options use the same risk-free rate and also expire on the same day. Let's run the calculation for all tickers!
premiums = [premium(c, data['s'], 0.05, 0.13778) for c in data['c'].items()]
AAPL: S=188.01, K=185.0, r=0.05, T=0.13778, type=C, sigma=0.25133422827795837, premium=9.264718563473352
GOOG: S=136.38, K=136.0, r=0.05, T=0.13778, type=C, sigma=0.3334488626006967, premium=7.37473047699028
AMZN: S=143.2, K=143.0, r=0.05, T=0.13778, type=C, sigma=0.3740810988798152, premium=8.49836139003888
NVDA: S=488.88, K=485.0, r=0.05, T=0.13778, type=C, sigma=0.5380555051571062, premium=42.312102122850916
TSLA: S=242.84, K=240.0, r=0.05, T=0.13778, type=C, sigma=0.5978797177153061, premium=23.576217613444044
LLY: S=588.54, K=585.0, r=0.05, T=0.13778, type=C, sigma=0.27668983620418824, premium=27.91609307266293
JPM: S=149.74, K=149.0, r=0.05, T=0.13778, type=C, sigma=0.21769958048869922, premium=5.730386079003452
XOM: S=103.66, K=104.0, r=0.05, T=0.13778, type=P, sigma=0.2622961333517632, premium=3.833220017212305
AVGO: S=975.4, K=975.0, r=0.05, T=0.13778, type=C, sigma=0.32762039500874146, premium=50.75180095398753
V: S=248.11, K=245.0, r=0.05, T=0.13778, type=C, sigma=0.18849603446983362, premium=9.517766751627079
JNJ: S=148.8, K=145.0, r=0.05, T=0.13778, type=C, sigma=0.16470111192176468, premium=6.468225702121728
PG: S=151.42, K=145.0, r=0.05, T=0.13778, type=P, sigma=0.15020283486133143, premium=0.8256978257766896
MA: S=396.83, K=395.0, r=0.05, T=0.13778, type=P, sigma=0.2085917915162287, premium=10.047835615842018
HD: S=308.19, K=305.0, r=0.05, T=0.13778, type=C, sigma=0.23516338551999078, premium=13.486783173128828
ADBE: S=595.31, K=590.0, r=0.05, T=0.13778, type=P, sigma=0.3491675706381003, premium=26.064754646338173
MRK: S=101.35, K=102.0, r=0.05, T=0.13778, type=P, sigma=0.19328049253425997, premium=2.8743774932946877
COST: S=596.78, K=595.0, r=0.05, T=0.13778, type=C, sigma=0.20399242233838977, premium=21.01916126285886
CVX: S=145.56, K=145.0, r=0.05, T=0.13778, type=C, sigma=0.2442523141032357, premium=6.049323730101676
ABBV: S=137.6, K=138.0, r=0.05, T=0.13778, type=P, sigma=0.1983861287795725, premium=3.765586371616962
WMT: S=169.78, K=165.0, r=0.05, T=0.13778, type=C, sigma=0.15528602884693177, premium=7.4949669107517
PEP: S=167.25, K=165.0, r=0.05, T=0.13778, type=C, sigma=0.1511472835108664, premium=5.639449037215996
KO: S=57.21, K=57.0, r=0.05, T=0.13778, type=C, sigma=0.14192521797403318, premium=1.5205345733456141
CSCO: S=53.28, K=53.0, r=0.05, T=0.13778, type=C, sigma=0.19798244935255943, premium=1.8953757827944173
CRM: S=219.42, K=220.0, r=0.05, T=0.13778, type=P, sigma=0.34361379918075297, premium=10.674541243742226
ACN: S=325.5, K=335.0, r=0.05, T=0.13778, type=C, sigma=0.26322917771381316, premium=9.542905510762864
NFLX: S=461.94, K=460.0, r=0.05, T=0.13778, type=C, sigma=0.42258542083434136, premium=31.338777464639946
MCD: S=270.39, K=265.0, r=0.05, T=0.13778, type=P, sigma=0.1397354070055457, premium=2.647640732711565
AMD: S=118.0, K=119.0, r=0.05, T=0.13778, type=P, sigma=0.4939505006751646, premium=8.717579117305945
BAC: S=29.62, K=30.0, r=0.05, T=0.13778, type=C, sigma=0.26238259593786306, premium=1.0688521096457375
ORCL: S=114.06, K=111.0, r=0.05, T=0.13778, type=P, sigma=0.27720520875055465, premium=2.940484621130132
CMCSA: S=42.53, K=42.0, r=0.05, T=0.13778, type=C, sigma=0.25278548226092584, premium=2.0189478694569836
PFE: S=30.19, K=30.0, r=0.05, T=0.13778, type=C, sigma=0.21768908588572533, premium=1.1774023755761256
ABT: S=98.0, K=98.0, r=0.05, T=0.13778, type=C, sigma=0.21193232700378156, premium=3.412365190342449
INTC: S=40.61, K=40.0, r=0.05, T=0.13778, type=C, sigma=0.38880430429409446, premium=2.7797631343870286
DIS: S=93.93, K=93.0, r=0.05, T=0.13778, type=C, sigma=0.3172399100887614, premium=5.202063523096449
VZ: S=36.0, K=35.0, r=0.05, T=0.13778, type=C, sigma=0.24141000756602202, premium=1.9799817175898546
WFC: S=42.84, K=42.0, r=0.05, T=0.13778, type=C, sigma=0.27876461422646787, premium=2.3662048640334774
AMGN: S=273.03, K=270.0, r=0.05, T=0.13778, type=C, sigma=0.21113599866532942, premium=11.12291516192144
QCOM: S=128.92, K=128.0, r=0.05, T=0.13778, type=C, sigma=0.35978479141741715, premium=7.752598665414411
COP: S=115.03, K=116.0, r=0.05, T=0.13778, type=P, sigma=0.3149581026890284, premium=5.453217092380683
IBM: S=152.58, K=152.5, r=0.05, T=0.13778, type=C, sigma=0.17697878513657805, premium=4.572054413530125
SPY: S=449.68, K=449.0, r=0.05, T=0.13778, type=C, sigma=0.15700684137533322, premium=12.399055722285766
QQQ: S=385.62, K=349.0, r=0.05, T=0.13778, type=C, sigma=0.21313815359347674, premium=40.20261193189299
Each line shows the symbol, spot price, strike, risk-free rate, time to expiry, vol and the premium for that particular option. Recall that the puzzle requires us to round all of the premiums to two decimal places and take the sum of the rounded premiums. The rounded_premiums variable shown below has that information for us. The only thing left is to sum the list of rounded premiums into a single number:
rounded_premiums = list(map(lambda x: round(x, 2), premiums))
sum(rounded_premiums)
463.28999999999996
Rounding it up, we reach 463.290 as the final answer 😁.
